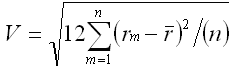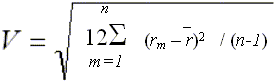Statistics Formulas |
|
|
The Risk Statistics formulas on this page are listed in alphabetical
order. |
|
Absolute Downside Risk
The annualized standard deviation of the negative account returns.
This measure is derived from at least 12 negative observations and may
require a longer period (e.g., 2-3 years) to calculate.
| Formula: |
Absolute Downside Risk- Account
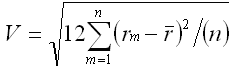
Where:
V = annualized variability of monthly
returns
rm = unannualized time weighted rate of
return in month m
rm < 0
n = number of months in time period
n > or = 12
_
r = average monthly rate of return
_
r < 0 |
| Formula: |
Absolute Downside Risk- Index
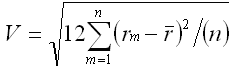
Where:
V = annualized variability of monthly
returns
rm = unannualized time weighted rate of
return in month m
rm < 0
n = number of months in time period
n > or = 12
_
r = average monthly rate of return
_
r < 0 |
Annualized Standard
Deviation - Account
The difference between the account total fund rate of return and the
benchmark rate of return.
| Formula: |
Annualized Standard Deviation (Portfolio)
Based on a Population
This is a measure of the variability of returns around the
average return of the portfolio. This measure is available after twelve
months of performance have passed; shorter periods do not provide a good
indication of a fund's variability.
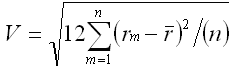
Where:
V = annualized variability of monthly
returns
rm = unannualized time weighted rate of
return in month m
_
r = average monthly rate of return
n = number of months in time period |
The standard deviation used to measure investment portfolios is the
squared deviations from the average of monthly returns, divided by the
number of observations (12 for one year, etc) with that product then multiplied
by the square of the frequency of returns used.
Monthly return frequency is the square root of 12, with 12 being months
in a year. The calculation uses the actual number of observations in the
denominator of the calculation, as opposed to the standard deviation of
a sample which uses n-1. It is an investment tenet that if you have two
portfolios with the same return, the one with a lower standard deviation
is more desirable, because the return was achieved with less risk.
| Formula: |
Annualized Standard Deviation (Portfolio)
Based on a Sample
This is a measure of the variability of returns around the
average return of the portfolio. This measure is available after twelve
months of performance have passed; shorter periods do not provide a good
indication of a fund's variability.
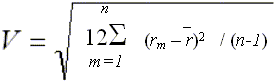
Where:
V = annualized variability of monthly
returns
rm = unannualized time weighted rate of
return in month m
_
r = average monthly rate of return
n = number of months in time period |
| Note: |
This calculation estimates Standard Deviation based on a sample. It
is a measure of how widely values are dispersed from the mean. The Standard
Deviation calculation that is based on a sample assumes that its arguments
are a sample of the population.
If available data represents the entire population, then standard deviation
should be computed using the calculation based on a population. |
Annualized Standard
Deviation - Index
| Formula: |
Annualized Standard Deviation (Index)
Based on a Population
This is a measure of the variability of returns around the
average return of the index. This measure is available after twelve months
of performance have passed; shorter periods do not provide a good indication
of a fund's variability.
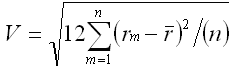
Where:
V = annualized variability of monthly
returns
rm = unannualized time weighted rate of
return in month m
_
r = average monthly rate of return
n = number of months in time period |
| Formula: |
Annualized Standard Deviation (Index)
Based on a Sample
This is a measure of the variability of returns around the
average return of the index. This measure is available after twelve months
of performance have passed; shorter periods do not provide a good indication
of a fund's variability.
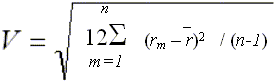
Where:
V = annualized variability of monthly
returns
rm = unannualized time weighted rate of
return in month m
_
r = average monthly rate of return
n = number of months in time period |
| Note: |
This calculation estimates Standard Deviation based on a sample. It
is a measure of how widely values are dispersed from the mean. The Standard
Deviation calculation that is based on a sample assumes that its arguments
are a sample of the population.
If available data represents the entire population, then standard deviation
should be computed using the calculation based on a population. |
Capture Ratio
| Formula: |
Down Market Capture Ratio Equation
((1+AR0 ) * (1+AR1 ) *
* (1+ ARn )) - 1/ ((1+ IR0 ) * (1+IR1 ) *
*
(1+IRn ))-1
Where:
AR = Account ROR
IR = Index ROR
IR < 0
n = number of periods |
| Formula: |
Up Market Capture Ratio Equation
((1+AR0 ) * (1+AR1 ) *
* (1+ ARn )) - 1/ ((1+ IR0 ) * (1+IR1 ) *
*
(1+IRn ))-1
Where:
AR = Account ROR
IR = Index ROR
IR > 0
n = number of periods |
Methodology for Producing Up Market and Down Market
Capture Ratios:
For any chosen time period there are X pairs or returns (account/consolidation
and index). For example, there will be 12 pairs of data for a one-year
time period.
Identify the up and down market pairs and separate them into two time
series. This is done by examining the index return for each pair result.
If the index return is greater than zero it is defined as an up market
result and conversely, if the return is less than zero it is put into
the down market time series.
For the up market time series, link the account results and then the
index results. (You don't need to annualize when there are more than 12
observations).
This produces the following ratio: linked account ror/linked index ror.
The ratio is then expressed as a percentage The same is done with the
down market times series.
| Note: |
If the result for Up Market Capture Ratio is < or = 0, a zero will
be displayed. If the result for the Down Market Capture Ratio is >
or = 0, a zero will be displayed. |
Correlation
This is a standard correlation calculation measure which should only
be performed on periods greater than one year. The dependant variable
could be fixed on the returns of the S&P 500 or we could allow clients
to select the index.
| Formula: |
Correlation to Index
Where X is the independent Variable, (portfolio return) and Y is the
dependent variable (index return).

|
Excess Return
The arithmetic difference between the account total fund rate of return
and the benchmark rate of return.
| Formula: |
Excess Return Equation
excess return = (monthly account total fund return) - (monthly benchmark
return) linked and annualized |
Kurtosis
Kurtosis characterizes the relative peakedness or flatness of a distribution
compared with the normal distribution. Positive kurtosis indicates a relatively
peaked distribution. Negative kurtosis indicates a relatively flat distribution.
| Formula: |
The following is the calculation of kurtosis:

The standard deviation used in this calculation is not annualized; we
cannot use the existing as a component of this calculation.
Note: Kurtosis on the normal distribution =
3 |
Maximum Drawdown
Maximum Drawdown is the greatest loss from peak monthly return to lowest
monthly return. This is a classic risk measure for hedge funds, often
cited by hedge fund managers.
| Formula: |
Maximum
Drawdown
MD = Min(X1, X1+X2,
, X1+X2+
XN, X2+X3+
XN,
,
,XN) |
Maximum Recovery
Maximum Recovery is the greatest gain from the lowest monthly return
to the peak return.
| Formula: |
Maximum Recovery
MD = Max(X1, X1+X2,
, X1+X2+
XN,
X2+X3+
XN,
, ,XN) |
Relative Return
A measure of the risk of deviating from the benchmark's return for the
period. A low tracking error indicates that there is a good match between
the benchmark and the account, calculated geometrically.
| Formula: |
Relative
Return Equation
relative return = [((1 + monthly account total fund return / 100) /
(1 + monthly benchmark return / 100)) -1] * 100 |
Sterling Ratio
The Sterling Ratio is a risk-reward measure which depicts the highest
returns with the least volatility. This measure is conceptually
similar to the Calmar ratio, but user the average drawdown of each annual
period. This measure is valid for three year periods and greater.
A higher value is desirable since it depicts higher return relative to
risk.
| Formula: |
Sterling Ratio
Sterling Ratio for three years = (D1+D2+D3)/3
Where: D1 is the max drawdown for the 1st 12 months, D2 is the max drawdown
for the 2nd 12 months, and D3 is the max drawdown for the 3rd 12months. |
Tracking Error
A measure of the risk of deviating from the benchmark's return for the
period. A low tracking error indicates that there is a good match between
the benchmark and the account.
| Formula: |
Tracking Error
tracking error = annualized standard deviation of ((account total fund
return) - (benchmark total fund return)) |
Historical Tracking Error is essentially the standard deviation of monthly
excess return the manager has generated over or under the index. The standard
deviation of the excess returns is annualized and the calculation uses
the actual number of observations as opposed to a sample calculation which
uses n-1.
| Note: |
Fundamentals displays two tracking error measures.
One is the standard historical tracking error calculation that uses
the standard deviation based on a population; the alternate calculation
uses standard deviation based on a sample.
For more information, see Annualized
Standard Deviation. |
Relative Tracking
Error
| Formula: |
Relative Tracking Error Equation
relative tracking error = annualized standard deviation of ((1 + account
total fund return / 100) / (1 + benchmark total fund return / 100))*100 |
Information Ratio
A measure of the incremental return earned by an account versus its
benchmark relative to the incremental risk assumed versus its benchmark.
| Formula: |
Information Ratio Equation
information ratio = (excess return) / (tracking error) |
| Note: |
Fundamentals displays two Information Ratio measures.
One is the standard calculation that uses a tracking error that is calculated
using the standard deviation based on a population. The alternate calculation
uses a tracking error that is calculated using the standard deviation
based on a sample.
For more information, see Annualized
Standard Deviation. |
Jensen's Alpha
A measure that involves an ordinary least squares regression return
to calculate risk-premium for an account's return against its benchmark.
A positive alpha means the account performed better than its benchmark
in risk-adjusted terms. A negative means the opposite.
| Formula: |
Jensen's Alpha Equation
Jensen's Alpha = [sum(square(X)) * sum(Y) - sum(X)sum(X * Y)] / [n *
sum(square(x)) - square(sum(X))]]
Where:
n = number of periods and n > 0
X = (benchmark return) - (risk-free return)
Y = (account total fund return) - (risk-free return) |
M Squared
M squared is the Risk-Adjusted Performance RAP(i) = risk-adjusted rate
of return for portfolio i.
| Formula: |
M Squared Equation
(M/i)(ri - rf) + rf
Where:
M = standard deviation of monthly
returns of the benchmark
i = standard deviation of monthly returns for portfolio i
ri = average monthly return of portfolio i
rf = risk-free rate of return (90 T-Bill rate for the month) |
R Squared
A measure that varies from 0.0 (meaning no correlation between the benchmark
and the account returns) to 1.0 for complete agreement between the two.
This measure is sometimes referred to as the coefficient of determination.
| Formula: |
R-Squared Equation
R-squared = square[(n * sum(X * Y)) - (sum(X) * sum(Y) / (sqrt((n *
sum(square(X))) - (square(sum(X)) * (sqrt((n * sum(square(Y))) - (square(sum(Y))]
|
Relative Downside Risk
The standard deviation of the negative results is the difference between
account returns and index returns. This measure is derived from at least
12 negative observations and may require a longer period (e.g., 2-3 years)
to calculate.
| Formula: |
Relative Downside Risk Equation
annualized standard deviation of ((account total fund return) - (benchmark
total fund return))
Where:
((account total fund return) - (benchmark total fund return)) < 0 |
Relative Volatility (Beta)
A measure that uses an ordinary least squares regression return to compute
the relative volatility of an account against its benchmark. A relative
volatility measure of 1.0 means equal volatility as the benchmark, greater
than 1.0 means more volatile, and less than 1.0 means less volatile.
| Formula: |
Relative Volatility Equation
Relative Volatility = [n * sum(X * Y) - (sum(X) sum(Y)] / [n * sum(square(X)
- square(sum(X)]
Where:
n = number of periods and n > 0
X = (benchmark return) - (risk-free return)
Y = (account total fund return) - (risk-free return) |
Risk Free Return
The rate of return from an investment that is considered risk-free or
very near risk-free. Risk free investments will vary from country.
The risk-free investment used in calculations for accounts and groups
with a US Dollar base currency is the 90 Day US T-Bill. Calculations for
non-US dollar based accounts and groups use the JP Morgan Cash Index in
the appropriate currency as the risk free investment.
Sharpe Ratio
A measure of the return earned per unit of risk.
This measure looks at the excess returns of an account relative to the
volatility of the account's returns.
| Formula: |
Sharpe Ratio Equation - Portfolio
Sharpe Ratio = (portfolio total fund return) - (risk free return) /
(annualized standard deviation of portfolio total fund return) |
This measure looks at the excess returns of an index relative to the
volatility of the index's returns.
| Formula: |
Sharpe Ratio Equation - Index
Index Sharpe Ratio = (index total return) - (risk-free return) / (annualized
standard deviation of index). |
| Note: |
Fundamentals displays two Sharpe Ratio measures.
One is the standard calculation using the standard deviation based on
a population. The alternate calculation uses standard deviation based
on a sample.
For more information, see Annualized
Standard Deviation. |
Skewness
Returns the skewness of a distribution. Skewness characterizes the degree
of asymmetry of a distribution around its mean. Positive skewness indicates
a distribution with an asymmetric tail extending toward more positive
values. Negative skewness indicates a distribution with an asymmetric
tail extending toward more negative values.
| Formula: |
Skewness

Where s is the standard deviation
The standard deviation used in this calculation is not annualized; we
cannot use the existing as a component of this calculation.
Note: Skewness on the normal distribution =
0 |
Sortino Ratio
The Sortino ratio is the excess return over risk-free rate over the
downside semi-variance. This ratio allows investors to go beyond simply
looking at excess returns to total volatility, since such a measure does
not consider how often the price of the security rises as opposed to how
often it falls.
| Formula: |
Sortino Ratio Equation
(AR - RF) / (DSR)
Where:
AR = account rate of return
RF = risk free index rate of return
DSR = downside risk |
Treynor Ratio
A risk-adjusted return measure that provides excess return per unit
of risk where risk is defined as systematic risk (beta).
| Formula: |
Treynor Ratio Equation
Treynor ratio = (account total fund return - risk free return) / (systematic
risk) |